Random Point in Radius with Spatial4J
Recently I needed to generate random points within a given radius around a point on a map.
I found it less obvious than I expected, so I decided to document the process here in case it helps anyone.
I’m using Spatial4J, a Java geospatial library which provides utilities for doing spatial operations in a geodesic context. In particular this contrasts with the also-popular Java Topology Suite, which provides vector-oriented geometric utilities in a Cartesian context.
For mapping work where you care about normal surface-of-the-earth distance units like feet or meters, Spatial4J is often the tool you need. That said, if you’re not working on the JVM, other great tools like Shapely (Python) and RGeo (Ruby) provide similar utilities for other languages.
Deps / Repl setup
I’m going to show some code snippets in scala which can be used interactively in the scala REPL.
For a real project, you’ll obviously want to put this into a pom/sbt/lein/whatever config file, but for quick experimentation, you can download the Spatial4J JAR from maven:
wget https://repo1.maven.org/maven2/org/locationtech/spatial4j/spatial4j/0.7/spatial4j-0.7.jar
Then in a scala repl, require it:
➸ scala
Welcome to Scala 2.12.2 (Java HotSpot(TM) 64-Bit Server VM, Java 1.8.0_121).
Type in expressions for evaluation. Or try :help.
scala> :require spatial4j-0.7.jar
Added '/private/tmp/spatial4j-0.7.jar' to classpath.
Now you’ll be able to import and work with Spatial4J’s classes in your REPL session.
Outline
We want to provide a center point (as a latitude and longitude) and a radius and get back a random point within the implied circle.
Here are the rough steps we’ll follow:
- Set up some imports
- Construct some basic spatial4j factory objects (it doesn’t have “4J” in the name for nothing)
- Make an s4j point representing our desired center lat/lon
- Pick a random distance offset within the desired radius
- Pick a random bearing (0 - 360 degrees) to shift our point
- Convert our distance (in meters) to an appropriate offset (in /degrees/) at the target lat/lon. We’ll get to this in a minute, but it turns out this has to be done in polar units like degrees rather than cartesian units like meters. Spatial4J provides a lot of utility here.
- Victory! Get back our new random point.
Imports
First, set up some imports:
import org.locationtech.spatial4j.context.SpatialContext
import org.locationtech.spatial4j.distance.DistanceUtils
Factory Stuff
Spatial4J uses a Factory object called a SpatialContext for many of its core APIs. There are a lot of different ways to configure this depending on your needs, but for the most common use-cases they include a static implementation under SpatialContext.GEO:
val context = org.locationtech.spatial4j.context.SpatialContext.GEO
Make a point object to represent the desired lat/lon
We’ll use another factory off of our SpatialContext to construct this. Remember in Geospatial tech longitude is X and latitude is Y:
val lat = 33.94
val lon = -118.41
val startPoint = context.getShapeFactory.pointXY(lon, lat)
Pick a random distance offset
val radius = 1000
val offsetMeters = scala.util.Random.nextDouble * radius
Pick a random bearing
val bearingDegrees = scala.util.Random.nextDouble * 360
Convert the linear distance offset to angular units (degrees)
This is the kicker for working with geodesic libraries like Spatial4J. It operates in a polar context, dealing with radii and angles (lat/lon) from the earth, but a distance like 500 meters is cartesian, dealing with flat distances on the earth’s surface.
Fortunately there are ways to convert between the 2. In particular Spatial4J’s DistanceUtils module includes some constants and utilities for this purpose:
val earthRadiusMeters = DistanceUtils.EARTH_MEAN_RADIUS_KM * 1000
val offsetDegrees = DistanceUtils.dist2Degrees(offsetMeters, earthRadiusMeters)
You might notice we are using Earth’s “mean radius” here. Depending on the level of precision required by your application, there are more sophisticated ways to make this conversion more accurate. For example the earth isn’t truly spherical but rather slightly oval-shaped, and algorithms exist to find a more precise radius at a given latitude rather than simply taking the mean. In keeping with blog post tradition, we’ll leave researching this as an exercise for the reader.
Get a new point
We now have a starting point, a bearing, and an offset radius in degrees.
Finally we can use another Spatial4J utility, org.locationtech.spatial4j.distance.GeodesicSphereDistCalc, to convert our start point, bearing, and offset to a new point.
Note that this uses a very Java-ish API, where you first construct the Point object yourself using a placeholder lat/lon and then pass it in to be modified by the Distance Calculator.
import org.locationtech.spatial4j.distance.GeodesicSphereDistCalc
val distCalc = new GeodesicSphereDistCalc.Vincenty
val newPoint = context.getShapeFactory.pointXY(0,0)
distCalc.pointOnBearing(startPoint, offsetDegrees, bearingDegrees, context, newPoint)
println(newPoint)
// Pt(x=-118.00099201867381,y=33.9950199965435)
All together
Now that we’ve seen the pieces, we can assemble them into a nice utility function:
import org.locationtech.spatial4j.context.SpatialContext
import org.locationtech.spatial4j.distance.{DistanceUtils, GeodesicSphereDistCalc}
import org.locationtech.spatial4j.shape.Point
object PointGenerator {
val context = org.locationtech.spatial4j.context.SpatialContext.GEO
val distCalc = new GeodesicSphereDistCalc.Vincenty
val earthRadiusMeters = DistanceUtils.EARTH_MEAN_RADIUS_KM * 1000
def randPointInRadius(lat: Double, lon: Double, radius: Double): Point = {
val startPoint = context.getShapeFactory.pointXY(lon, lat)
val offsetMeters = scala.util.Random.nextDouble * radius
val offsetDegrees = DistanceUtils.dist2Degrees(offsetMeters, earthRadiusMeters)
val bearingDegrees = scala.util.Random.nextDouble * 360
val newPoint = context.getShapeFactory.pointXY(0,0)
distCalc.pointOnBearing(startPoint, offsetDegrees, bearingDegrees, context, newPoint)
newPoint
}
}
scala> PointGenerator.randPointInRadius(34.0,-118.0,500)
res1: org.locationtech.spatial4j.shape.Point = Pt(x=-118.00141054557675,y=33.9971987911845)
scala> PointGenerator.randPointInRadius(34.0,-118.0,500)
res2: org.locationtech.spatial4j.shape.Point = Pt(x=-117.99966381772931,y=33.997181705450046)
scala> PointGenerator.randPointInRadius(34.0,-118.0,500)
res3: org.locationtech.spatial4j.shape.Point = Pt(x=-118.0008673083813,y=33.99933155556646)
scala> PointGenerator.randPointInRadius(34.0,-118.0,500)
res4: org.locationtech.spatial4j.shape.Point = Pt(x=-117.99862804930764,y=34.001770697901655)
A catch regarding distributions
This works great, but if we take a large sample and plot it on a map, we’ll notice the points cluster tightly near the center:
(0 to 1000).map(_ => PointGenerator.randPointInRadius(33.94,-118.41,2000)).map(p => s"${p.getY},${p.getX}").foreach(println)
// 33.93769610837791,-118.39618482618667
// 33.944086950586815,-118.41270519841264
// 33.938436141001375,-118.41187357399744
// 33.93224346396654,-118.39866113148551
// etc
// Copy + paste | geoq map
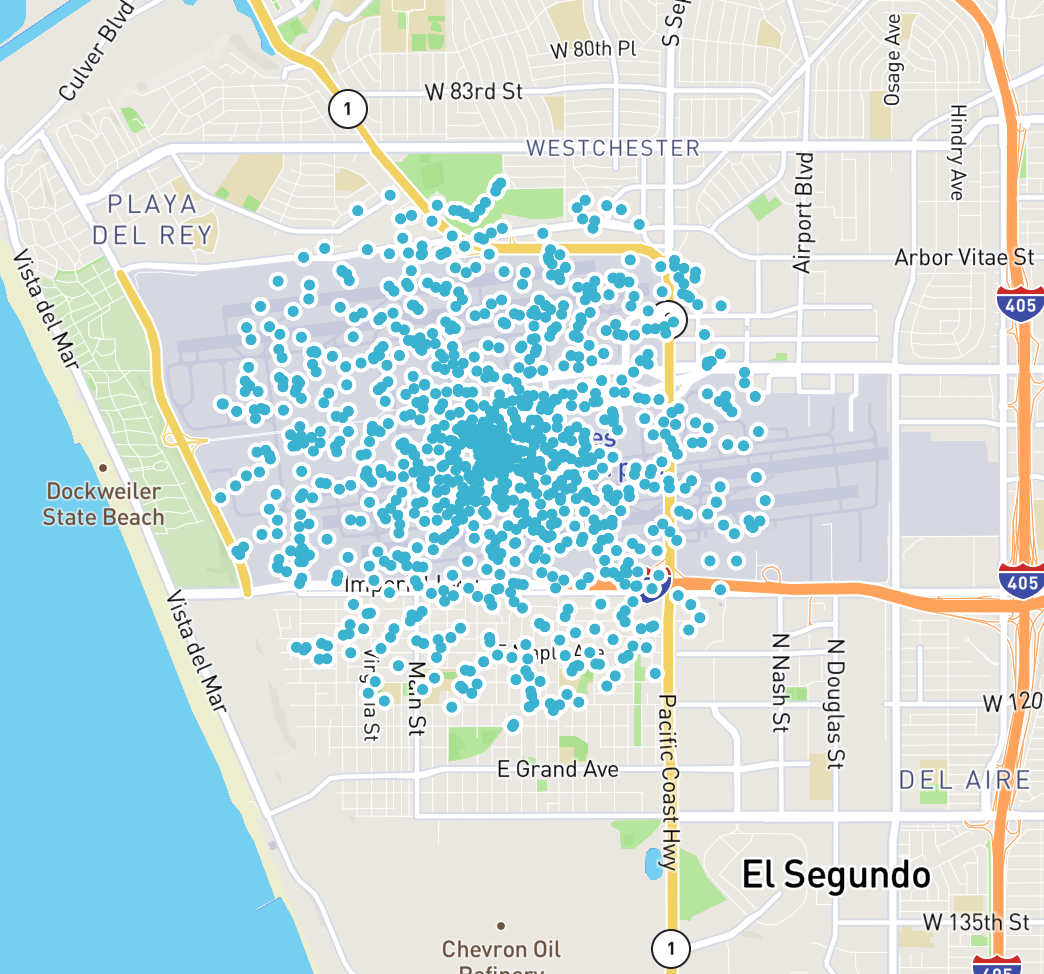
It turns out that because of the way circles and area work, taking a random distance offset within our desired radius doesn’t give a uniform distribution throughout the circle, but rather clusters the points toward the center.
If we want a smooth distribution over the area described by our point and radius, we’ll need to sample radii exponentially weighted toward the max radius. That is, we want:
val offsetMeters = scala.math.sqrt(scala.util.Random.nextDouble) * radius
We could even give our users an option to toggle between these choices when using the function:
import org.locationtech.spatial4j.context.SpatialContext
import org.locationtech.spatial4j.distance.{DistanceUtils, GeodesicSphereDistCalc}
import org.locationtech.spatial4j.shape.Point
import scala.util.Random
import scala.math
object PointGenerator {
val context = org.locationtech.spatial4j.context.SpatialContext.GEO
val distCalc = new GeodesicSphereDistCalc.Vincenty
val earthRadiusMeters = DistanceUtils.EARTH_MEAN_RADIUS_KM * 1000
def randPointInRadius(lat: Double, lon: Double, radius: Double, evenDistribution: Boolean): Point = {
val startPoint = context.getShapeFactory.pointXY(lon, lat)
val offsetMeters = if (evenDistribution) {
math.sqrt(Random.nextDouble) * radius
} else {
Random.nextDouble * radius
}
val offsetDegrees = DistanceUtils.dist2Degrees(offsetMeters, earthRadiusMeters)
val bearingDegrees = Random.nextDouble * 360
val newPoint = context.getShapeFactory.pointXY(0,0)
distCalc.pointOnBearing(startPoint, offsetDegrees, bearingDegrees, context, newPoint)
newPoint
}
}
Sampling from this distribution gives us the smooth coverage we might have expected:
(0 to 1000).map(_ => PointGenerator.randPointInRadius(34.0,-118.0,2000, true)).map(p => s"${p.getY},${p.getX}").foreach(println)
// 33.939640262698276,-118.43135364227057
// 33.946446329758274,-118.4285590217258
// 33.927846243486826,-118.40795788351743
// 33.922739829504145,-118.41091483844558
// 33.93132724358199,-118.41135336156653
// 33.941905760094876,-118.42909622711291
// 33.939879012731645,-118.39112410484391
// etc...
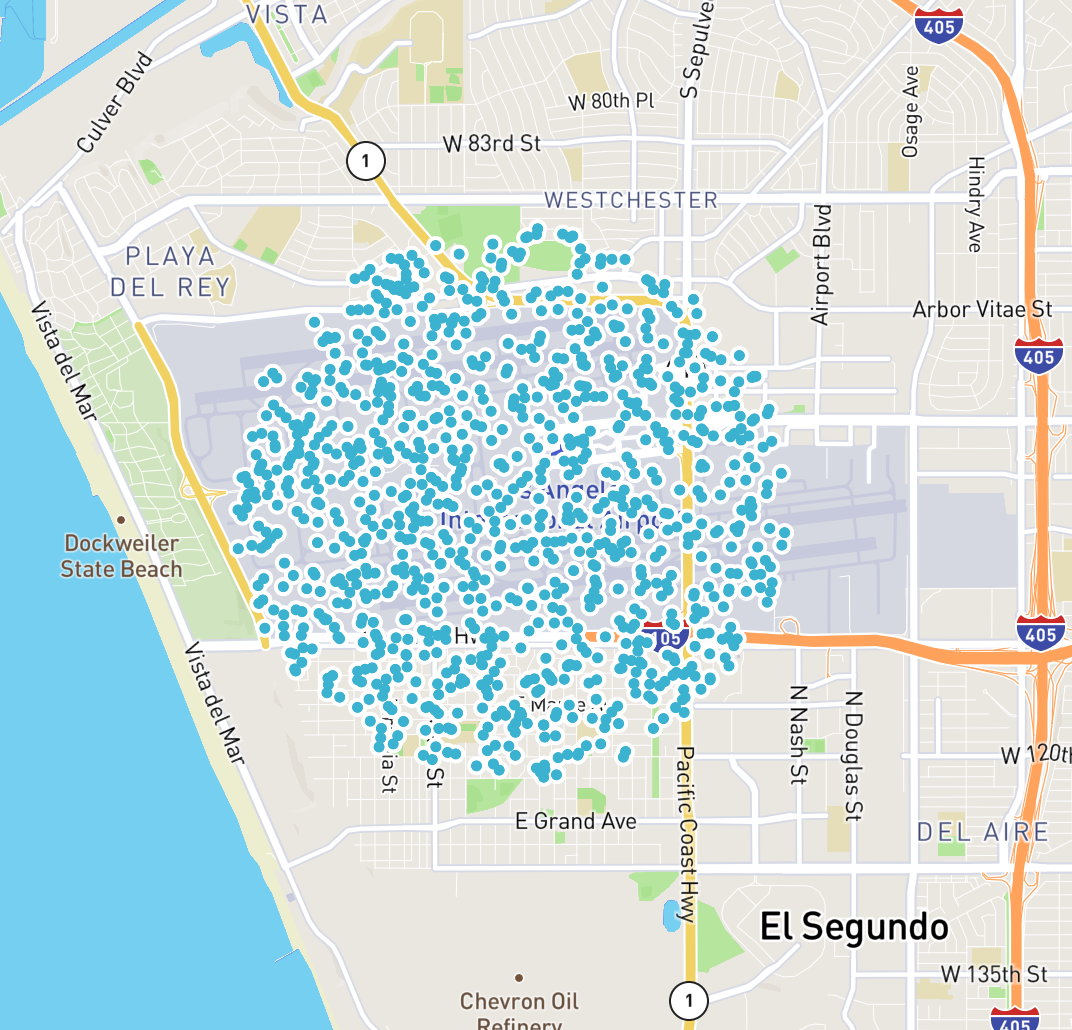
And that’s it! A utility like this is helpful for applications like generating heatmaps, so hopefully it will be useful to you:

Finally, if you happen to be working in clojure, the great Factual/geo library includes a utility exactly like this: geo.spatial/rand-point-in-radius.